Cook Abstand

Statistik
Autor:in

Norman Markgraf

Veröffentlichungsdatum

29. Juni 2020

Geändert

25. Juli 2025

Frage: Was macht einen Wert zum Ausreißer?

Eine mögliche Antwort lautet: Ein Wert gilt als Ausreißer, wenn er deutlich von den übrigen Werten abweicht und einen (starken) Einfluss auf das Modell ausübt.

Ein Verfahren zur Identifikation solcher Ausreißer ist der Cook-Abstand (engl.: Cook’s distance). Die zugrunde liegende Idee besteht darin zu messen, wie stark ein einzelner Wert das Modell beeinflusst. Dazu vergleicht man das Modell einmal mit und einmal ohne diesen Wert.

Sehen wir uns den Cook-Abstand anhand eines einfachen linearen Regressionsmodells näher an:

Vorbereitungen

Wir nutzen das Paket mosaic, daher laden wir es zunächst:

library(mosaic)

Falls die tipping-Daten nicht lokal vorliegen, werden sie aus dem Internet geladen:

if (!file.exists("tips.csv")) {
  download.file("https://goo.gl/whKjnl", destfile = "tips.csv")
}

Nun werden die Daten eingelesen:

tips <- read.csv2("tips.csv")

Für unser Modell verwenden wir nur die Variablen total_bill und tip:

tips %>% select(c("total_bill", "tip")) -> tips

Unser Modell:

Zuerst ein Streudiagramm zur Visualisierung der Daten:

gf_point(tip ~ total_bill, data = tips)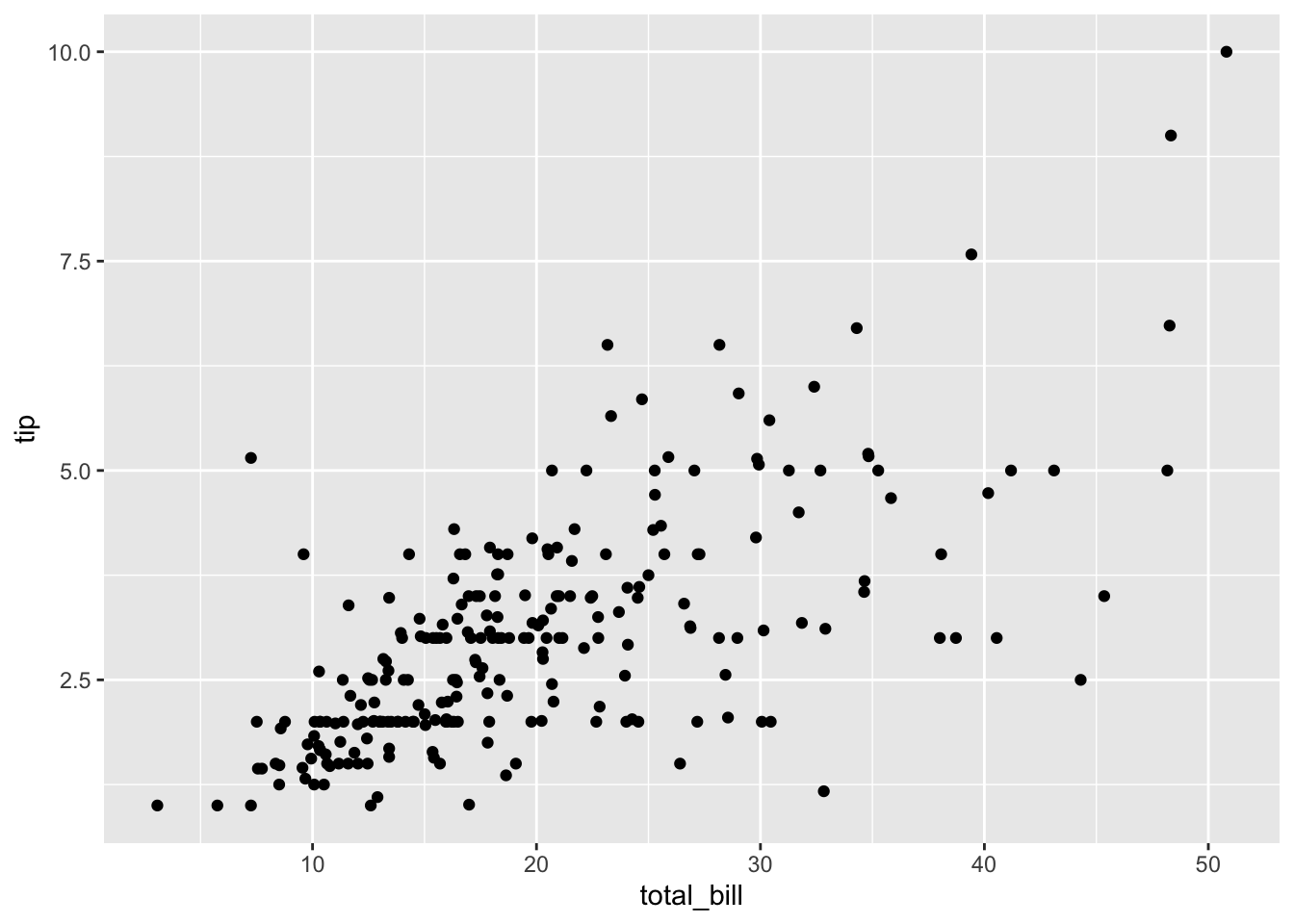

Dann erstellen wir ein lineares Regressionsmodell:

erg_lm <- lm(tip ~ total_bill, data = tips)
summary(erg_lm)

Call:
lm(formula = tip ~ total_bill, data = tips)

Residuals:
    Min      1Q  Median      3Q     Max 
-3.1982 -0.5652 -0.0974  0.4863  3.7434 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 0.920270   0.159735   5.761 2.53e-08 ***
total_bill  0.105025   0.007365  14.260  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.022 on 242 degrees of freedom
Multiple R-squared:  0.4566,    Adjusted R-squared:  0.4544 
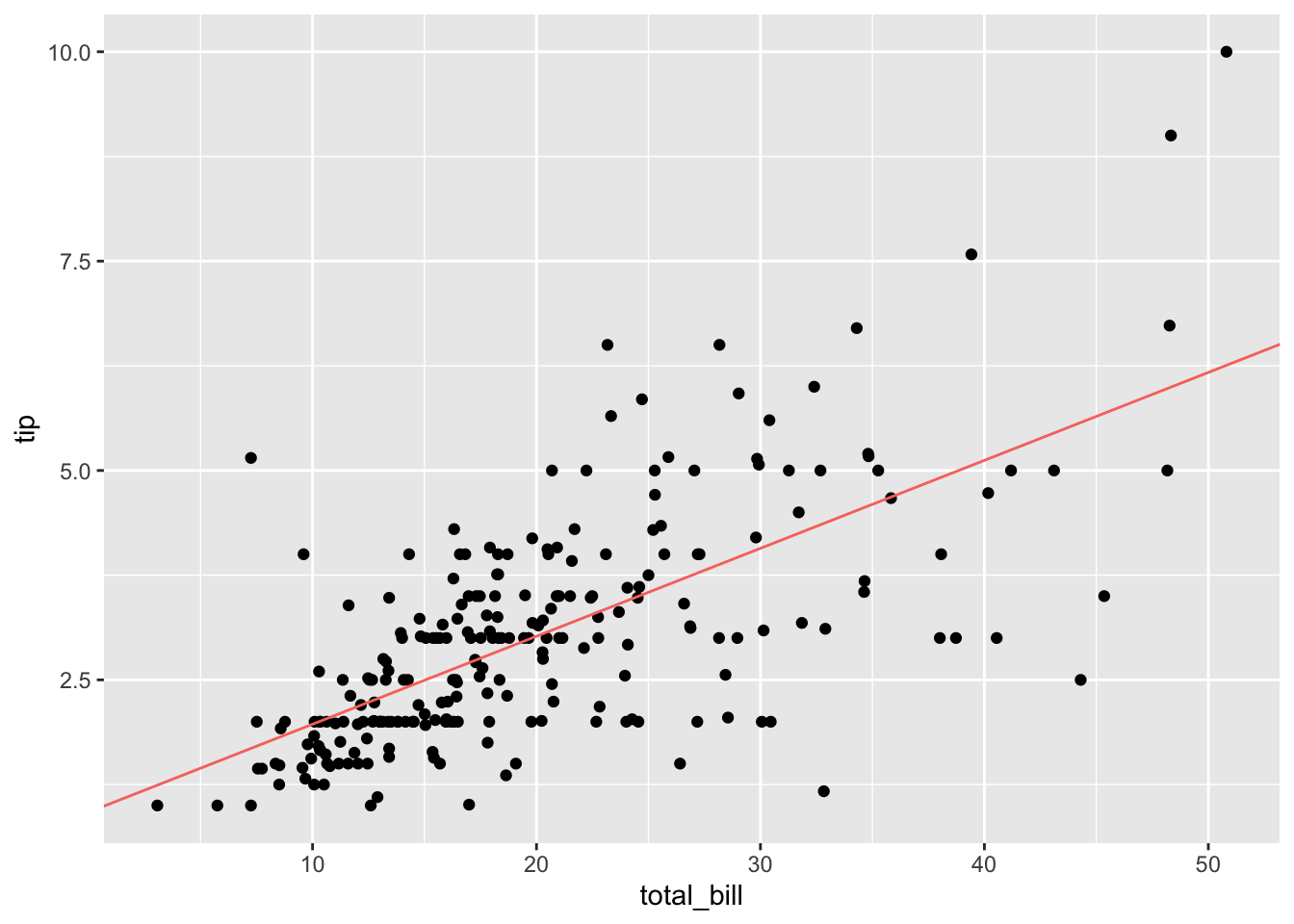
F-statistic: 203.4 on 1 and 242 DF,  p-value: < 2.2e-16

Visualisierung der Regressionsgeraden:

gf_point(tip ~ total_bill, data = tips) %>%
  gf_coefline(
    model = erg_lm,
    color = ~ "Regressionsgerade",
    show.legend = FALSE
  )

Einflussreiche Ausreißer können bei linearen Modellen problematisch sein. Was passiert, wenn wir einen potenziellen Ausreißer entfernen?

Beispiel: Wir eliminieren die Beobachtung mit dem Index 173

tips %>% slice(173) -> tips_removed
tips_removed
  total_bill  tip
1       7.25 5.15
tips %>% slice(-173) -> tips_red
erg_lm_red <- lm(tip ~ total_bill, data = tips_red)
summary(erg_lm_red)

Call:
lm(formula = tip ~ total_bill, data = tips_red)

Residuals:
    Min      1Q  Median      3Q     Max 
-3.2136 -0.5351 -0.0818  0.4951  3.6869 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  0.86065    0.15709   5.479 1.08e-07 ***
total_bill   0.10731    0.00723  14.843  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.9992 on 241 degrees of freedom
Multiple R-squared:  0.4776,    Adjusted R-squared:  0.4754 
F-statistic: 220.3 on 1 and 241 DF,  p-value: < 2.2e-16

Grafischer Vergleich:

gf_point(tip ~ total_bill, data = tips_red) %>%
  gf_coefline(
    model = erg_lm,
    color = ~ "Regressionsgerade"
    ) %>%
  gf_point(
    tip ~ total_bill, 
    colour = ~ "Entfernter Punkt",
    data = tips_removed)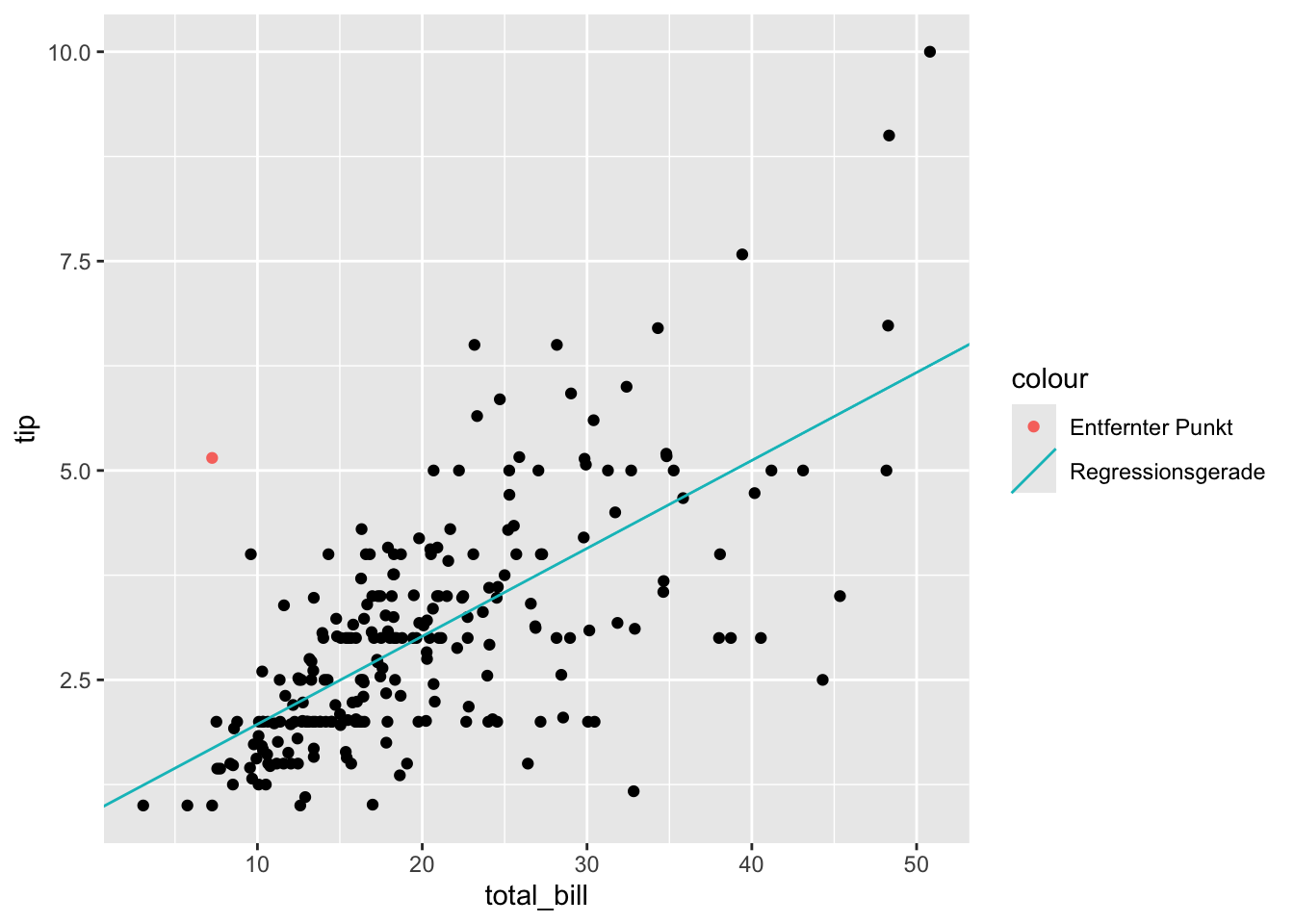

Berechnung des Cook-Abstands

Wir vergleichen die Prognosen beider Modelle:

new_data <- tibble(total_bill = tips$total_bill)
prognose_lm <- predict(erg_lm, newdata = new_data)
prognose_lm_red <- predict(erg_lm_red, newdata = new_data)

Berechnung:

\[ d_j = \sum_{i=1}^n \left(\hat{y}_i - \hat{y}_{i(j)}\right)^2 \] Dabei ist \(\hat{y}_i\) die Prognose des Wertes \(y_i\) auf Basis von \(x_i\) mit dem Originalmodell und \(\hat{y}_{i(j)}\) die Prognose wenn man die \(j\)-te Beobachtung aus dem Modell gestrichen hat.

d_j <- sum((prognose_lm - prognose_lm_red)^2)
d_j
[1] 0.1511406

Der Cook Abstand \(D_j\) wird nun noch normiert durch \[{\text{var}_{\text{cook}}} = p \cdot s_{\epsilon_i^2}^2\] Dabei ist \(s_{\epsilon_i^2}^2\) der erwartungstreue Schätzer der Varianz der Residuen und \(p\) die Anzahl aller erklärenden Variablen plus Eins, also: $ 1 + 1 = 2$.

Normierung des Cook-Abstands:

\[ D_j = \frac{d_j}{\text{var}_{\text{cook}}} = \frac{\sum\limits_{i=1}^n \left(\hat{y}_i - \hat{y}_{i(j)}\right)^2}{p \cdot s_{\epsilon_i^2}^2} \]

# Summary des Modells
selm <- summary(erg_lm)

# Wir finden p als rank im Modell
p <- erg_lm$rank 

# Wir finden den erwatungtreuen Schätzer im Summary des Modells
s_quad_eps_quad <- (selm$sigma)^2 

var_cook = p * s_quad_eps_quad

D_j = d_j / var_cook
D_j
[1] 0.07234504

Alternativ kann der Wert direkt mit cooks.distance() berechnet werden:

cooks.distance(erg_lm)[173]
       173 
0.07234504

Wann aber ist nun ein Wert ein einflussreicher Ausreißer?

Entscheidungskriterien

Cook selber gibt dafür die Bedingung \(D_j > 1\) an. Andere Autor*innen schreiben \(D_j > 4/n\), wobei \(n\) die Anzahl der Beobachtung ist.

In unserem Beispiel liefert die Variante \(D_j > 1\)

cooks <- cooks.distance(erg_lm)
names(cooks) <- NULL
n <- nrow(tips)

any(cooks > 1)
[1] FALSE

keinen Ausreißer.

Wenn wir jedoch mit \(D_j > 4/n\) suchen .

any(cooks > 4/n)
[1] TRUE

dann gibt es Ausreißer.

Die Indices dieser finden wir mit:

which(cooks > 4/n)
 [1]  24  48  57 103 142 157 171 173 179 183 184 185 188 208 211 213 215 238

Daten bereinigen:

remove <- which(cooks > 4/n)
tips %>% slice(-remove) -> tips_no_outliers
tips %>% slice(remove) -> tips_removed
erg_lm_no_outliers <- lm(tip ~ total_bill, data = tips_no_outliers)

Ergebnis des Modells:

summary(erg_lm_no_outliers)

Call:
lm(formula = tip ~ total_bill, data = tips_no_outliers)

Residuals:
     Min       1Q   Median       3Q      Max 
-2.22592 -0.48166 -0.06794  0.46992  2.31414 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 0.773324   0.139435   5.546  8.2e-08 ***
total_bill  0.111799   0.006958  16.069  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.7778 on 224 degrees of freedom
Multiple R-squared:  0.5355,    Adjusted R-squared:  0.5334 
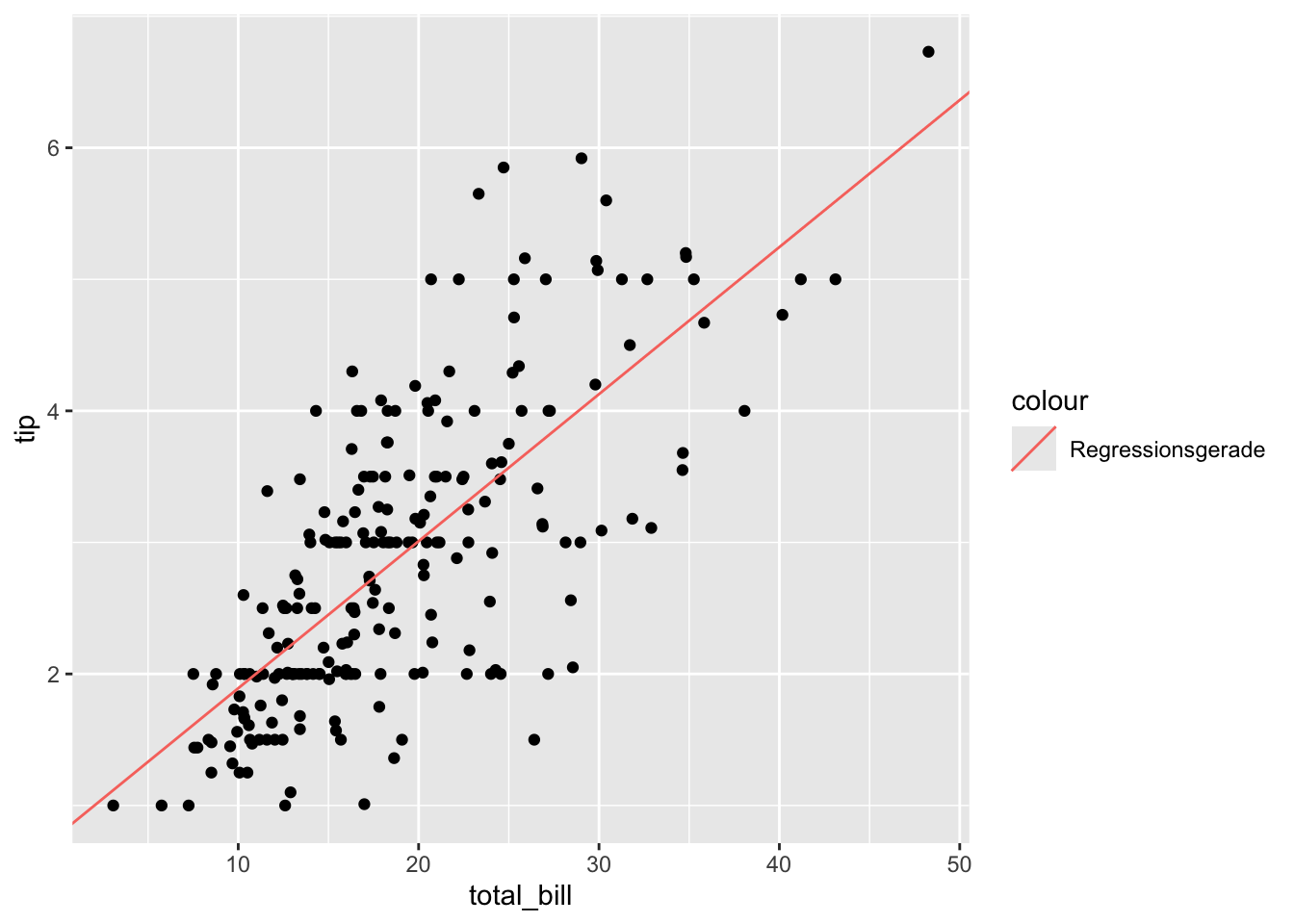
F-statistic: 258.2 on 1 and 224 DF,  p-value: < 2.2e-16

Daten bereinigen:

gf_point(tip ~ total_bill, data = erg_lm_no_outliers) %>%
  gf_coefline(
    model = erg_lm_no_outliers, 
    color = ~"Regressionsgerade"
  )

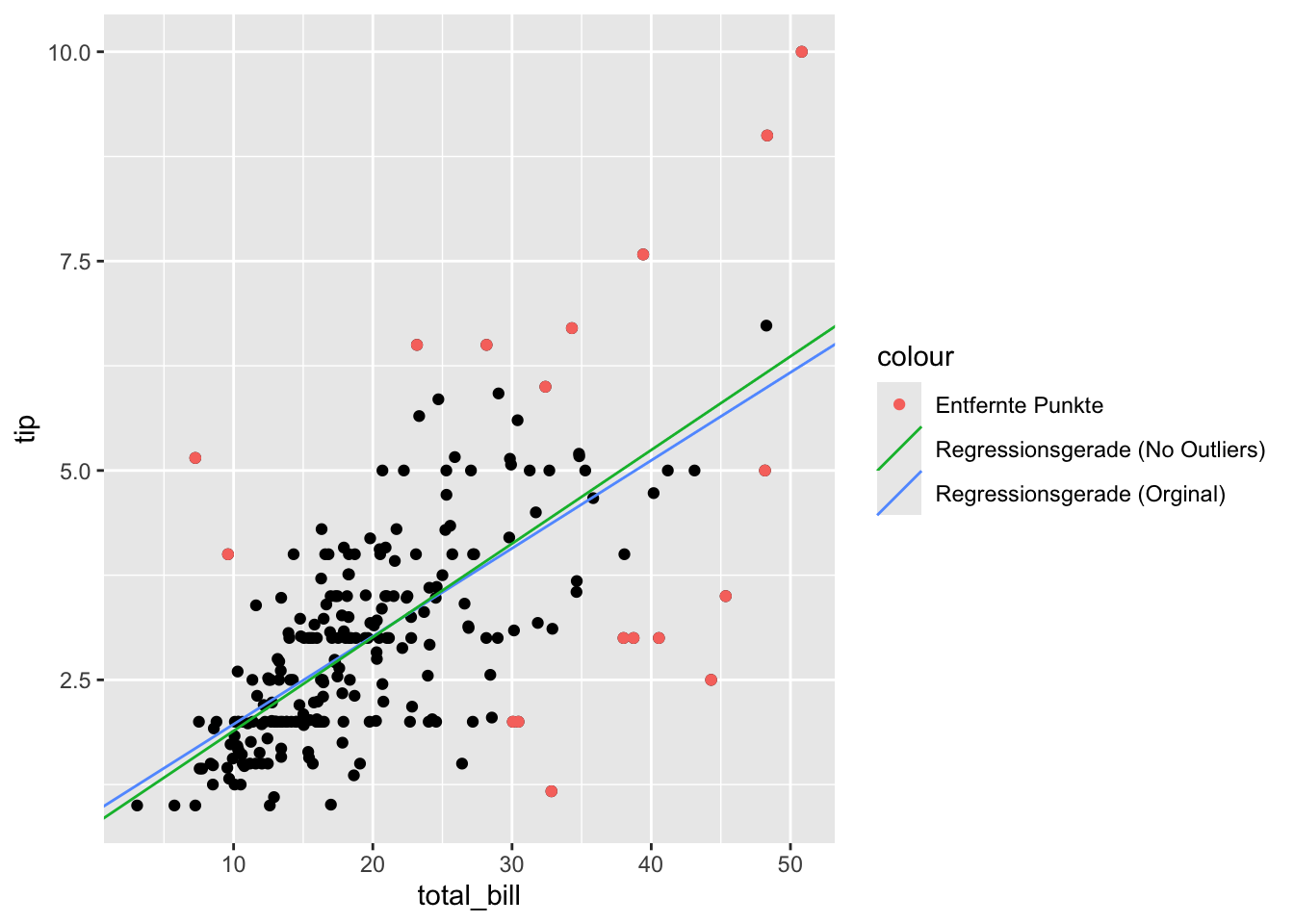
Grafischer Vergleich beider Modelle:

gf_point(tip ~ total_bill, data = erg_lm) %>%
  gf_coefline(
    model =  erg_lm,
    color = ~ "Regressionsgerade (Orginal)"
  ) %>%
  gf_coefline(
    model = erg_lm_no_outliers,
    color = ~ "Regressionsgerade (No Outliers)"
  ) %>%
  gf_point(
    tip ~ total_bill,
    color = ~ "Entfernte Punkte",
    data = tips_removed
  )

Modelle in Gleichungsform

Das ursprüngliche Modell:

\[ \widehat{tips}_{lm} = 0.9202696 + 0.1050245 \cdot total\_bill \]

Das um pot. Ausreißer bereinigte Modell:

\[ \widehat{tips}_{lm\_no} 0.7733236 + 0.1117985 \cdot total\_bill \]